Fundamentals of Machine Learning

In Deep Learning Part 1 and 2, we learned about the fundamentals of neural networks and how forward propagation (forward pass) works. In this article, we will learn how neural networks learn from experience through backpropagation (backward pass).

Backpropagation (Backward Pass)

Backpropagation (Backward Pass) is the process of learning that the neural network uses to adjust the network weights and minimize error.

Initially, weights in a network are set to random numbers, so the initial model is not accurate with high error. Backpropagation is needed to improve this accuracy progressively.

We need to find out how much each node in a layer contributes to the overall error. This can actually be done through backpropagation. The idea is to adjust the weights in proportion to their error contribution in order to eventually reach an optimal set of weights. The gradient descent algorithm is actually what is used to adjust the weights.

Gradient Descent

The goal is to gradient descent is to find the set of weights that minimize the loss function. Optimization functions calculate a gradient to do this. A gradient is the partial derivative of the loss function with respect to the weights. In other words, it is how much a small increase in the weights will affect the loss function. Weights are adjusted in the opposite direction of the calculated direction. Think of this as taking a step towards the local minimum of a function f(x). This cycle is repeated until we reach a minimum of the loss function.

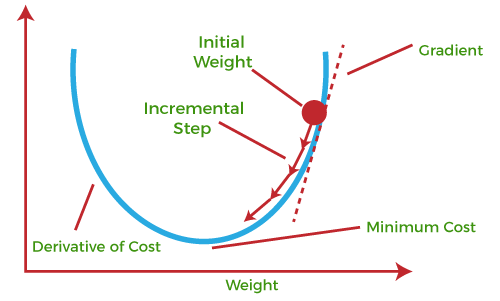
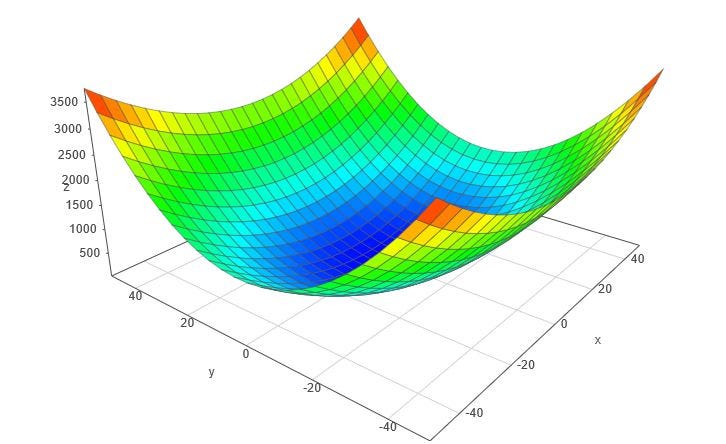
Note: Gradient descent is not guaranteed to find the absolute minimum in a function, as it could land on a relative minimum that doesn’t have as small a loss as the absolute minimum.

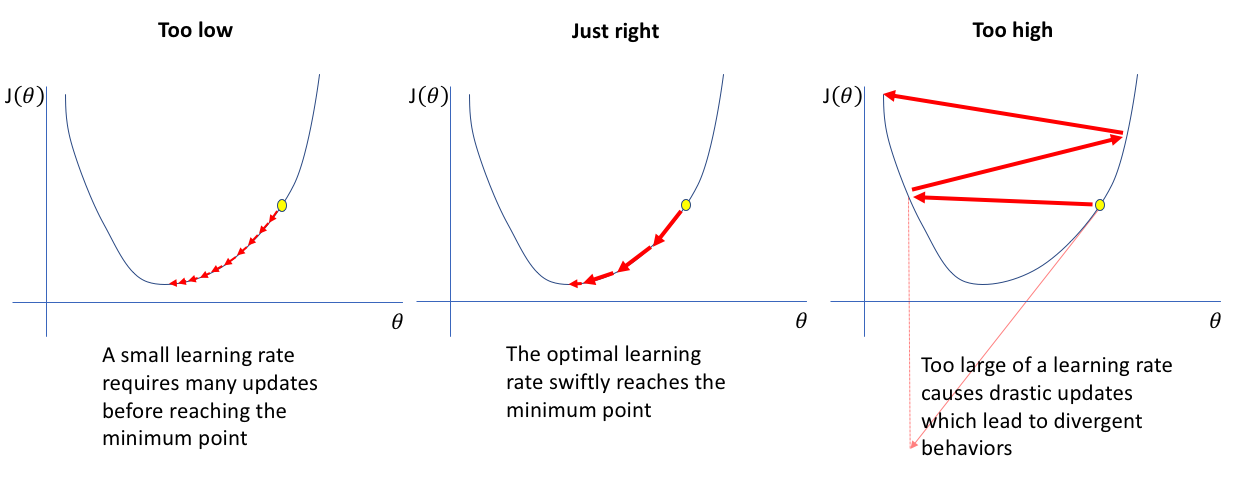
The learning rate is a hyperparameter that determines the step size (the amount by which weights are updated each time). A high learning rate can jump over minima, which is not ideal. A low learning rate will approach the minima too slowly, requiring many iterations of the model. We can try out different learning rates with trial and error to improve results.

Overfitting

Unfortunately, deep neural networks are prone to overfitting the training data and producing poor accuracies on the test data. One technique to mitigate overfitting is batch normalization, which consists of normalizing inputs. This can improve the performance and stability of neural networks.

Another technique is dropout, which is randomly shutting down a fraction of the layer’s training step (resetting their values to 0). This prevents the neurons from having too much dependency on each other. Below is a visual of the dropout method.

Types of Neural Networks

There are various types of neural networks. Three main ones are artificial neural networks (ANNs), recurrent neural networks (RNNs), and convolutional neural networks (CNNs). ANNs specialize in simple tasks, RNNs in natural language processing and time data, and CNNs in image data.